Jandos Mambetali

Расширение арифметических операций

Ссылка на .PDF файл в гугл диске Расширение_арифметических_операции.pdf



   В этой статье предлагается возможность расширения арифметических операции сложения и умножения. Приводятся общие формулы характерные для таких операции, а также примеры их реализации.

Введение

Для начала введем множество символов для обозначения арифметических операции:

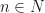, , , , , ...,  ,   операции увеличения чисел, если числа больше единицы.

, 
,  
, 
,  
 ....,   операции уменьшения чисел, если числа больше единицы.

где  - означает операцию сложения,  - означает операцию умножения,  - означает операцию возведения в степень.

 - означает операцию вычитания,  - означает операцию деления,  - означает операцию извлечение корня.

Примеры для :

Введенные символы, записанные в верхнем индексе  --- означают 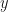 количество итерации данной операции. Пример:

Определяющие формулы

Для любых  и операции , \,  должны выполнятся равенства:

(1)

(2)

Примеры, следствия и предположения

Пример для формулы (1) :

Тогда, для предположительной операции  и  :

И для любого  :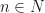

Fibonacci numbers in binary system

We get the sequence of Fibonacci numbers by slightly changing the binary number system – let’s do the conversion. Example:
$(n)_{notation}$
$(5)_{10}=(101)_2$
How we will transform: we will replace zeros with ones, ones with twos, then we sum them up. $101\rightarrow 212 \rightarrow 5$
$(6)_{10}=(011)_2 \rightarrow 122 \rightarrow 5$
$(7)_{10}=(111)_2 \rightarrow 222 \rightarrow 6$
Let’s write in two columns the numbers before the conversion, and after:
$0\rightarrow 1$ ; $1\rightarrow 2$ ; $2\rightarrow3$ ; $3\rightarrow4$ ; $4\rightarrow4$ ; $5\rightarrow5$ ; $6\rightarrow5$ ; $7\rightarrow6$ ; $8\rightarrow5$ ; $9\rightarrow6$ ; $10\rightarrow6$ ; $11\rightarrow7$
The numbers on the right are repeated, let’s count their repetitions:
$1\rightarrow1$ ; $2\rightarrow1$ ; $3\rightarrow1$ ; $4\rightarrow2$ ; $5\rightarrow3$ ; $6\rightarrow5$ ; $7\rightarrow8$ ; $8\rightarrow13$ ;
We get a sequence of Fibonacci numbers.
To derive a formula for Fibonacci numbers, you need to count the number of repetitions of the number. I note that each repeated number $n$ (converted from a binary number) occurs in the natural series of numbers in the interval $\min=floor \left( \frac{n+1}{2} \right)$ ; $\max=2^{n-1}$ ;
Let’s take the repeating number $8$ as an example. In how many ways can we write the number $8$ as a sum of twos and ones?
$1+1+1+1+1+1+2$
$1+1+1+1+2+2$
$1+1+2+2+2$
$2+2+2+2$
Subtract one deuce from each of the options:
$1+1+1+1+1+1$
$1+1+1+1+2$
$1+1+2+2$
$2+2+2$
For each case, we calculate the number of combinations from $n$ (the number of numbers) by $k$ (the number of twos), and sum them up. We get:
$\sum_{k=0}^{floor \left( \frac{n-2}{2} \right) } ( \frac{(n-(k+2))!}{(n -(2k+2))!\cdot k!} )$
Wikipedia only mentions diagonal summation in Pascal’s triangle.

ГИПОТЕЗА РАСШИРЯЮЩАЯ ПОСТУЛАТ БЕРТРАНА

Так как теорема Сильвестра обобщает постулат Бертрана, новая гипотеза расширяет постулат Бертрана.
Итак:
Между $x-1$ и $y+1$ существует нечётное число $k$ не делящееся без остатка ни на одно простое число $p$ равное или меньшее $(y-x)$ ; $p\leqslant(y-x)$ ; $k\ne0 \mod(p)$ , где

$(y-x)\leqslant x<y$

, $(y-x)>2$ ;
Из верности этой гипотезы следует верность гипотезы Лежандра, так как наименьший простой делитель для составных чисел до $n^2=y+1$ не превышает $n=(y-x)$ .
При $(y-x)=x$ гипотеза равнозначна постулату Бертрана.

ГИПОТЕЗА РАСШИРЯЮЩАЯ ПОСТУЛАТ БЕРТРАНА

Так как теорема Сильвестра обобщает постулат Бертрана, новая гипотеза расширяет постулат Бертрана.
Итак:
Между $x-1$ и $y+1$ ~~существует~~ нечётное число $k$ не делящееся без остатка ни на одно простое число $p$ равное или меньшее $(y-x)$ ; $p\leqslant(y-x)$ ; $k\ne0 \mod(p)$ , где $(y-x)\leqslant x <y$ , $(y-x)>2$ ;

Upd: (14.08.2020)

Гипотеза неверна, найден контрпример.

При $(y-x)=x$ гипотеза равнозначна постулату Бертрана.

на pari/gp проверял только конечную разность первого порядка составных чисел, не превышающих $\frac{primorial(y+1)}{2}$ , делящихся на простые $primes(y-x)$ кроме чётного простого 2, и обнаружил палиндромность последовательности из этой разности:
Пример:

{a=[0];

for(i=1, 106, if(Mod(i, 3)==0||Mod(i,5)==0||Mod(i,7)==0, a=concat(a,i) ) );
for(i=1, #a-1, print1(a[i+1]-a[i], ", ") )
}

3, 2, 1, 1, 2, 1, 2, 2, 1, 3, 2, 1, 3, 1, 2, 1, 2, 3, 2, 1, 
3, 1, 2, 3, 3, 1, 1, 1, 3, 1, 1, 1, 3, 3, 2, 1, 3, 1, 2, 3, 
2, 1, 2, 1, 3, 1, 2, 3, 1, 2, 2, 1, 2, 1, 1, 2, 3,

$A=(n_1, n_2, ... , n_i)$ ; $1<n_x\leqslant P_n\#$ ; $\wedge$ $n_x\equiv 0 \mod (p \in primes(n))$ ;
элементы кортежа $b$ : $b[k]=A[k+1]-A[k]$

( $P_n\#$ – праймориал до числа $n$ )

Collatz conjecture in reverse

photo clickable

Suppose we have such a Collatz fraction:

$\frac{\frac{2^{k_i}-1}{3} \cdot 2^{k_{i-1}}-1}{3}_{{...}_{\frac{\frac{2^{k_2}-1}{3} \cdot 2^{k_1}-1}{3}}}$

which is equal to a natural number. Then, for each power of two $2^{k_x}$ we have many other degrees of the form $2^{k_x+(\frac{2}{3}*3^{x})n}$ , $n\geqslant 1, n \in N$ ; any of which can replace the power of two $2^{k_x}$ and get another integer (natural) fractional solution.
$k_1, k_2, ... , k_i$ – Are different natural numbers.

Example:
$k_1=\{0, 2, 4, 6, 8, 10, ...\}$
$k_2=\{2, 8, 14, 20, 26, ...\}$
$k_3=\{2, 20, 38, 56, ...\}$
for: ${\frac{\frac{\frac{2^{k_3}-1}{3} \cdot 2^{k_2}-1}{3} \cdot 2^{k_1}-1}{3}}$

Depending on the $n$ , we equate the result of calculating such a fraction to $A_{n_x}$ , then the relations of finite differences $A$ will be:
$\frac{A_{n_x+1}-A_{n_x}}{A_{n_x}-A_{n_x-1}}=2^{\frac{2}{3}*3^{x}}$
where $x$ this is a subscript exponent $K$ associated with $n$ , (the index of the power of two of the variable part of the fraction).

First post was on forum https://dxdy.ru/topic133348-15.html